CONTENT

xRISC 3L

This computer has been designed and built over one weekend in ~2013/05 by two excited ~16 year olds: me, and one M. Dreef.

Grotesquely silly and inefficient in design in retrospect, it was nonetheless whipped up very quickly, and we still happen to be somewhat proud of it all these years later. :3

Not RISC-like whatsoever.

Perhaps OneDay™ there will be a v2, addressing all the mistakes mentioned here while retaining most of the soul of the previous design.

This article is quite unfinished

Features

• 4 general-purpose registers
• Unusual register-mapped ALU hogging the remaining 4 register locations
• 8 powerless instructions
• Program memory
  • 64 x 14-bit instructions
  • Could be expanded to 256, maybe.
• Very slow instruction cycle
• Output printer!
  • Just prints in binary whatever’s on the output.
• No inputs
  • Inputs were added later, but those later versions of the map have since been since lost.

Design

The Silly Architecture

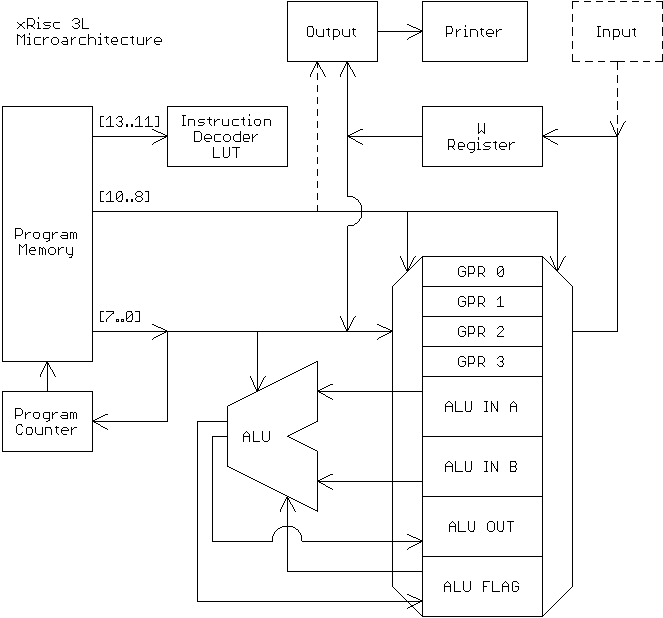
The Silly Instruction set

The instruction set of the x3L is very simple, containing only 8 mushy instructions:

The general bitwise structure of each instruction word is described by this pattern: AAABBBDDDDDDDD, where:

• AAA are the topmost 3 bits signifying the “op-code”,
• BBB typically signifies the source or target register,
• DDDDDDDD is used for 8-bit literals for data loads and jumps.

The opcodes are the following:

• 000 = NOPE
  • Does nothing. Very useful.
• 001 = MVLR
  • Move literal D to register B.
• 010 = MVRW
  • Move data from register B to W-register.
• 011 = MVWR
  • Move data from W-register to register B.
• 100 = WPRT
  • Print data in W-register.
  • Used as a general output instruction
  • Once extended with direction bit in LSB of B:
    • 0 = Write, 1 = Read?
    • Not implemented in presented version.
• 101 = ALUO
  • Perform an ALU operation specified by D.
  • The ALU is a blatant copy of the ALU specified in nand2tetris chapter 2.
  • This takes values from the ALU input registers, and generates a new ALU output and flags.
• 110 = JUMP
  • Unconditional jump to address specified by D.
• 111 = JIWZ
  • Conditionally jump to address specified by D if W-resiter is zero.
  • Surprisingly, this was the only condition to jump on.
  • Perhaps it would’ve been smart to multiplex condition sources with B, to perhaps jump on the ALU flags/input readiness?

The Silly Register map

All registers are readable and writeable, there is 8 that are accessible by the B index:

• 000 - General Purpose Register
• 001 - Ditto
• 010 - Ditto
• 011 - Ditto
• 100 - ALU A Input Register
• 101 - ALU B Input Register
• 110 - ALU Output Register
• 111 - ALU Flag Register

There’s also the moderately useless W-register, serving as an intermediary for all moves. Not sure how necessary W-register’s existence was at all, it only slows down moves even more…

ALU Operation Codes

The bits of the ALU operation bits (coming from D) are mapped like so:

• 0 = zx
  • x' = zx ? 0 : ina
• 1 = nx
  • x = nx ? !x' : x'
• 2 = zy
  • y' = zy ? 0 : inb
• 3 = ny
  • y = ny ? !y' : y'
• 4 = f
  • out' = f ? (x+y) : (x&y)
• 5 = no
  • out = no ? !out' : out'
• 6 and 7 are unused.

These function of the ALU is identical to the one mentioned in nand2tetris chapter 2. This also mentions useful configurations of the ALU operation bits.

Some code samples

These code samples are provided as-is, as they have been found from the ages long passed.

Some assembler quirks:

• All values are in hexadecimal. There was no prefix to distinguish decimal/hexadecimal numbers. Hex only.
• Labels were not supported by the assembler, so the addresses had to be calculated manually, and are always absolute.
• The assembler did not have any aliases for ALU operations; one always had to type out the operation code.

Fibonacci Numbers

Sources available here:

• FIBONA~1.X3 (earlier version)
• FIBONA~2.X3 (version below)

MVLR 4, 00		;Setup initial values
MVLR 5, 01
ALUO 40			;Add X and Y
MVRW 5			;Move Y to X
MVWR 4
MVRW 6			;Move OUT to Y
MVWR 5
WPRT			;Output
JUMP 02

Multiplier

Source available here:

• MULT.X3

MVLR 0,03			;stuff you want to multiply
MVLR 1,08			;stuff you want to multiply with - 1
MVLR 2,00			;clear the output register
	MVRW 1			;LOOP:
	JIWZ 12			;JIWZ END
	MVRW 0
	MVWR 4
	MVRW 2
	MVWR 5
	ALUO 08			;00001000 - X+Y
	MVRW 6
	MVWR 2
	MVRW 1
	MVWR 4
	ALUO 31			;00111000 - X-1
	MVRW 6
	MVWR 1
	JUMP 03			;JUMP LOOP
	MVRW 6			;END:
	WPRT
	JUMP 14			;DEAD, JUMP DEAD

The code above is said to be equivalent to the C pseudocode below:

;while(r1 != 0){
;	r2 = r2 + r1;
;	r1--;
;}
;print(r2);

The Silly Assembler

• XRISC3~1.JAR

One may use an extremely simple Java 7-based assembler to assemble the .x3 files above.

To use it, call it from the command line like so: java -jar xrisc3Lcompiler.jar [path to .x3 file]

The result will be .x3hex file created in the same directory as the .x3 file. This file will contain assembled binaries used as a template for manual placement of redstone torches into the program memory.

Sample output with the Fibonacci program above:

001 100 00000000
001 101 00000001
101 000 01000000
010 101 00000000
011 100 00000000
010 110 00000000
011 101 00000000
100 000 00000000
110 000 00000010

Possible Revamps?

There are quite some small tweaks that could’ve made this machine a bit less painful to use and somewhat more powerful.

Perhaps one day we’ll pick this up again and tweak it?

This article is unfinished

A few things are missing:

• Map download
• Mention of server tools used to build this
  • craftbukkit, worldedit
• More pictures
• A better description of the architecture
• Some overview/demo video